中上川 友樹 教授

| 所属 | 湘南工科大学 工学部 情報工学科 (2023年度から湘南工科大学 情報学部 情報学科 情報工学専攻 予定) 湘南工科大学大学院 工学研究科 電気情報工学専攻 |
| 学部研究テーマ | 有限集合やグラフなどの離散的な数学モデルに関する研究 |
| 大学院研究テーマ | グラフを用いた数学モデルに関する研究 離散構造のラムゼー型問題に関する研究 離散構造の数え上げに関する研究 |
研究概要
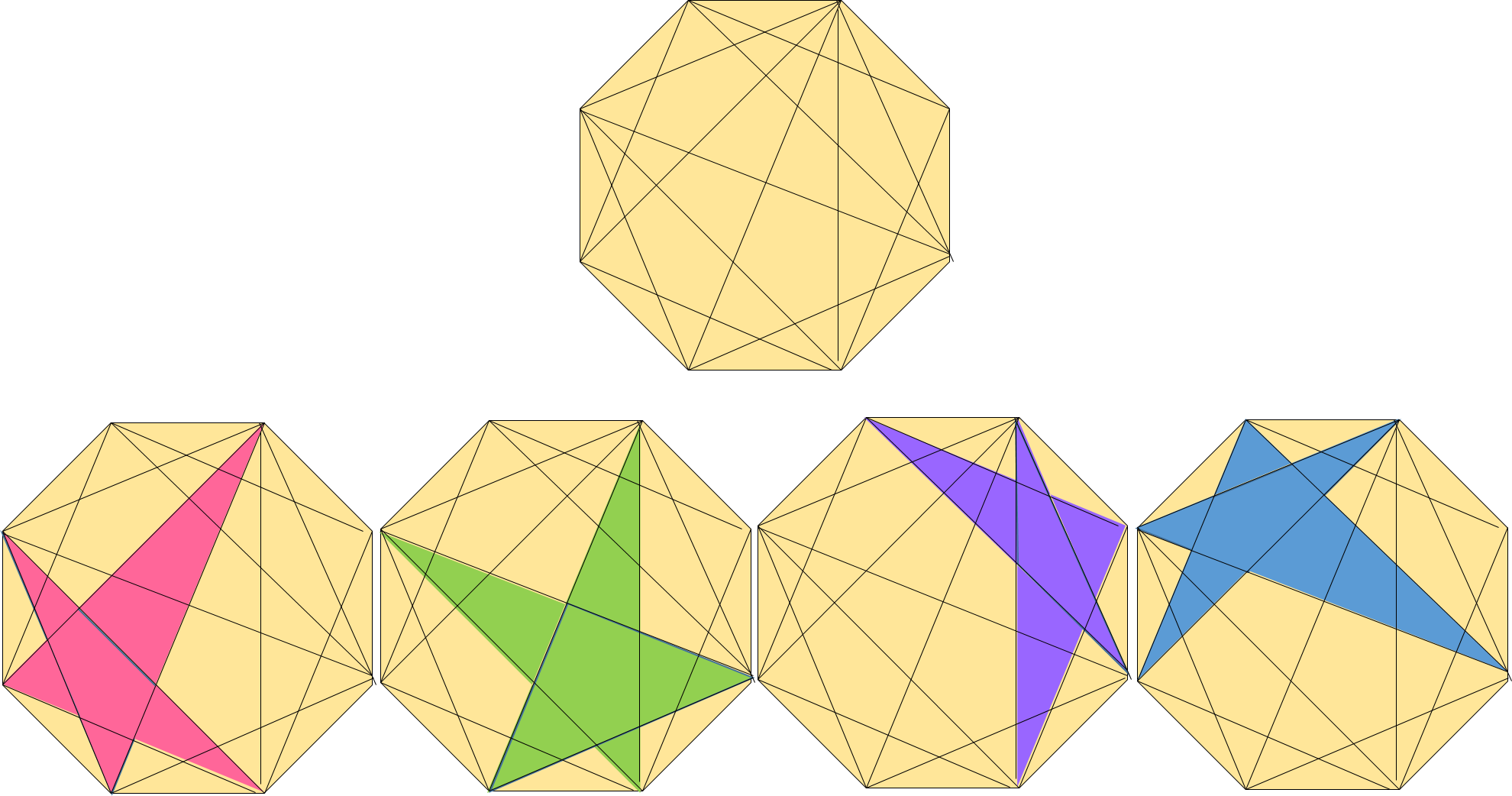
正8角形の2-三角形分割とそれに含まれる星形多角形
円の内部で交わる弦の交差を考察しています.本研究の目的は,与えられた交差条件を満たす弦の集合に関して,以下の問題を明らかにすることです. (a) 条件を満たす弦の集合の構造を組合せ論の手法により解明すること(特徴付け問題).(b) 条件を満たす弦の集合の個数を求めること(数え上げ問題).(c) 条件を満たす弦の集合の位数(その集合に含まれる弦の本数)の最大値または最小値を求めること(極値問題).
本研究の対象―弦とその交差―は,古来より初等的な平面幾何学で扱われてきたものですが,近年の研究により,その深く豊かな代数的構造が明らかにされつつあります.本研究の意義は,一見素朴に見える対象を組合せ論的な視点からとらえ直すことにより,それが数学のさまざまな分野に結びつく基本的な構造であることを示すことにあります.
本研究の対象―弦とその交差―は,古来より初等的な平面幾何学で扱われてきたものですが,近年の研究により,その深く豊かな代数的構造が明らかにされつつあります.本研究の意義は,一見素朴に見える対象を組合せ論的な視点からとらえ直すことにより,それが数学のさまざまな分野に結びつく基本的な構造であることを示すことにあります.
教育研究活動
<主な卒業研究テーマ>
・基本対称式を用いた魔方陣の探索, 円魔方陣の探索
・べき乗和とベルヌーイ数の研究
・一般化された完全数について
・円周率の公式における収束速度の比較研究
<主な担当科目>
・離散数学,線形代数,プログラミングのための基礎解析,幾何学2
<主な所属学会>
・日本数学会(応用数学分科会)
・基本対称式を用いた魔方陣の探索, 円魔方陣の探索
・べき乗和とベルヌーイ数の研究
・一般化された完全数について
・円周率の公式における収束速度の比較研究
<主な担当科目>
・離散数学,線形代数,プログラミングのための基礎解析,幾何学2
<主な所属学会>
・日本数学会(応用数学分科会)
